Images from the free space simulator Celestia (licensed under the GNU General Public License v2.0).
Introduction The Sky from Earth Celestial Coordinate Systems The Seasons and the Constellations The Galaxy Relating the Two Pictures Modeling the Relation References
When trying to visualize the Earth's position in space, there are two common pictures. The first depicts the solar system in empty space, with the sun at the center and the planets revolving around it. Relative to distances within the solar system, everything else in the galaxy is so far away that the stars are imagined as being on a so-called "celestial sphere" located infinitely far away and centered on the solar system. This is the view of space we are most familiar with. (Click images to enlarge.)
The second picture places the solar system among the structure of the Milky Way Galaxy. Here, instead of being afloat in infinite abstract space, we occupy a definite position relative to the rest of the galaxy.
But how do these two pictures relate? What is the orientation of the Earth's orbit relative to the plane of the galaxy? What direction do the constellations lie in as seen from "above" the galaxy? Where is the Earth at different times of the year in relation to these constellations? The answers - or the tools to find them - are out there, but I have never seen them all put together in one place. I therefore set out to do so myself.

The solstices and equinoxes (see below) have been used as markers of time since early in human history, and are known as the cardinal points. In the first millennium B.C., the Sun was in Aries on the vernal equinox and this location became known as the First Point of Aries [1]. Although the Sun's position on the vernal equinox shifts over time due to precession, the name "First Point of Aries" for the location of the vernal equinox on the celestial sphere has remained.
For our purposes the First Point of Aries is significant because it is used as the primary axis of both the geocentric-equatorial and ecliptic coordinate systems. From this point, the second axis of each system lies 90° east along the coordinate system's fundamental plane, and the third axis is perpendicular to both as given by the right-hand rule.
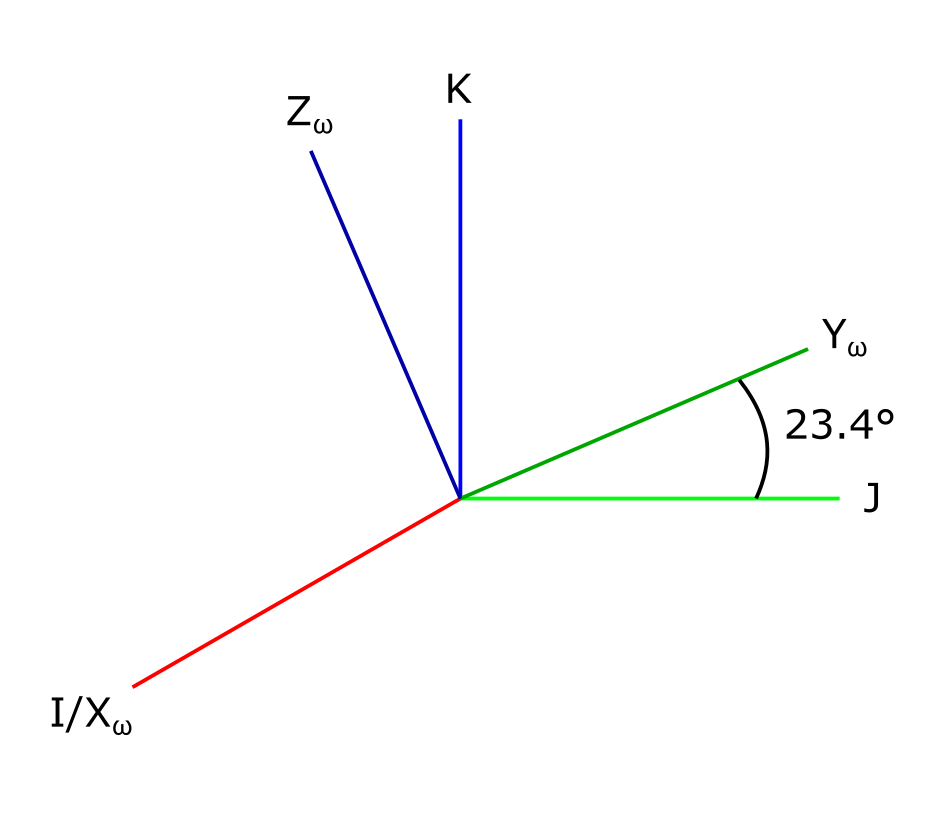
This coordinate system uses the Earth's equator, projected into space, as the fundamental plane. For this reason, it is inherently geocentric, unlike the ecliptic coordinate system (which can be helio- or geo-centric). The origin is at the Earth's center. The î-axis points toward the Sun's position on the vernal equinox, and the ĵ-axis lies 90° east of it. The k̂-axis points along the Earth's axis of rotation towards the Celestial North Pole (CNP). On this page, the letters I, J, and K will be used for the î-, ĵ-, and k̂-directions.
In this coordinate system the fundamental plane is the ecliptic. As seen from Earth, this is the Sun's apparent path across the sky over the year. From the Sun, the ecliptic is simply the plane of Earth's orbit. As stated above, use of the ecliptic as the fundamental plane allows this coordinate system to be centered at either the Sun or Earth. [2] (In the discussion on this webpage, the geocentric version will be used.) The x̂-axis points to the Ecliptic North Pole (ENP), which is perpendicular to the plane of the Earth's orbit. [3]. Following Mueller, Bate, and White [6], these directions are identified here as Xω, Yω, and Zω.
The geocentric-equatorial and ecliptic systems share an î-axis. The other two axises are tilted along this axis by 23.5°, like so:
The position of an object in the galaxy can be described relative to the Solar System's position in what are known as galactic coordinates. These consist of two values. The galactic longitude l indicates the angle of the object in the plane of the galaxy relative to the line between the Solar System and the galaxy's center. The galactic latitude b gives the angle between the galactic plane and the object, as measured from the Solar System.
It is common to see the seasons presented relative to the Earth's orbit in diagrams like this:
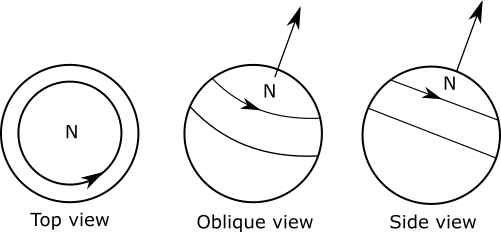
Earth spins on its axis once every 24 hours. [5] A point on Earth's surface can be imagined as tracing out a circular path over the course of this timespan, like this ("N" indicates the northern hemisphere):
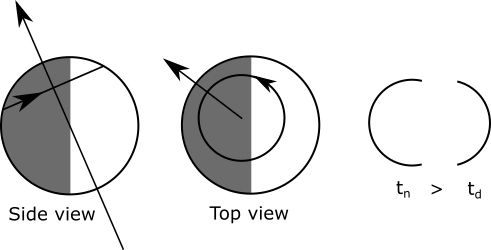
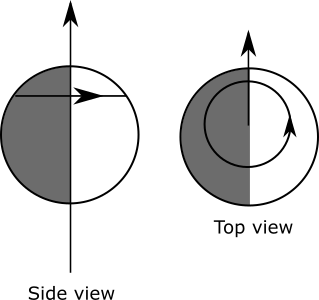
The first point of Aries anchors the ecliptic and equatorial coordinate systems among the constellations. It also fixes Earth's axis of rotation relative to its orbit. Relating Earth's position over the period of its orbit to the celestial coordinate systems is therefore straightforward. We need to know where in the Xω-Yω plane the boundaries of each constellation are in order to make a map of the constellations relative to Earth's orbit. [projection into I-J plane as seen from above]
I used the free astronomy software Stellarium to find the intersection of the ecliptic with each of the Zodiacal constellations. Ecliptic longitude was estimated visually to the arcminute, which is enough accuracy for the model's purposes. The data below are the boundaries of the ecliptic's path through each constellation in the direction of the Sun's path (increasing ecliptic longitude). Arcminute values were converted to decimal for plotting.
Ecliptic longitude (deg min) Ecliptic longitude (decimal)
Pisces 351 56 28 59 351.93 28.98
Aries 28 59 53 42 28.98 53.70
Taurus 53 42 90 26 53.70 90.43
Gemini 90 26 118 17 90.43 118.28
Cancer 118 17 138 20 118.28 138.33
Leo 138 20 174 09 138.33 174.15
Virgo 174 09 218 06 174.15 218.10
Libra 218 06 241 21 218.10 241.35
Scorpius 241 21 247 56 241.35 247.93
Ophiuchus 247 56 266 32 247.93 266.53
Sagittarius 266 32 299 57 266.53 299.95
Capricornus 299 57 327 47 299.95 327.78
Aquarius 327 47 351 56 327.78 351.59
To connect the months with the cardinal points, we first need to know where they start and end in degrees. I used a 365-day year for simplicity, and used the ending day of the year for each month to determine the degree at which the month ends.
Month Days End day Year fraction at end Degree at end
Jan 31 31 0.085 30.575
Feb 28 59 0.162 58.192
Mar 31 90 0.247 88.767
Apr 30 120 0.329 118.356
May 31 151 0.414 148.932
Jun 30 181 0.496 178.521
Jul 31 212 0.581 209.096
Aug 31 243 0.666 239.671
Sep 30 273 0.748 269.260
Oct 31 304 0.833 299.836
Nov 30 334 0.915 329.425
Dec 31 365 1.000 360.000
The Xω-axis is at 0° by definition. This usually falls on March 20th, the 79th day of the year. Therefore, the year starts 79/365th of a full circle (77.918°) counterclockwise from the Xω-axis. I rotated the month divisions by this amount to yield the final month-constellation-season diagram, as seen from above the Earth's orbital plane:
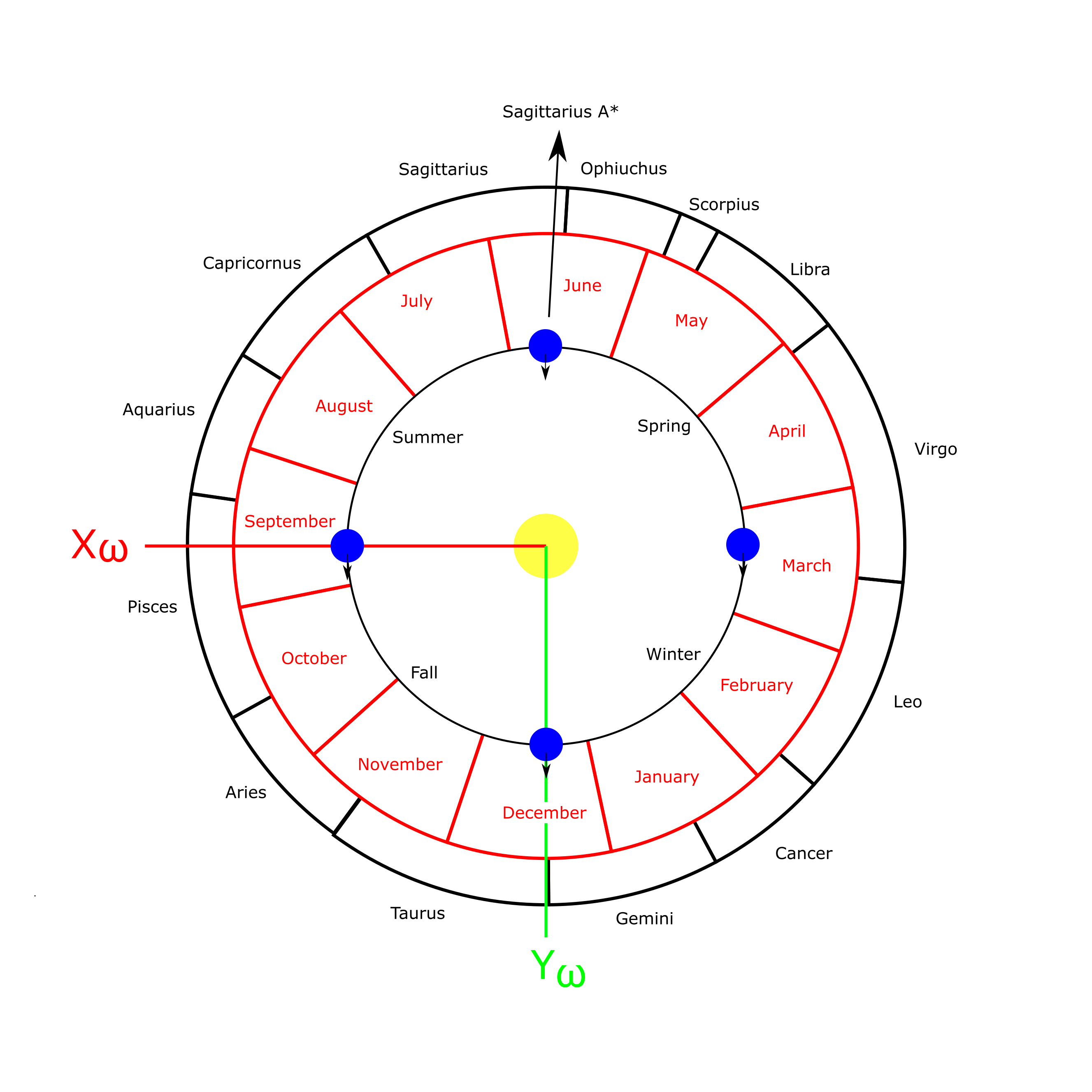
The Milky Way Galaxy is [description]. Our solar system is located [where], [distance] from the galactic center. The center of the galaxy, as seen from Earth, lies in the constellation Sagittarius and is known as Sagittarius A* (Sagittarius A-Star), abbreviated Sgr A*.
[diagram of location]
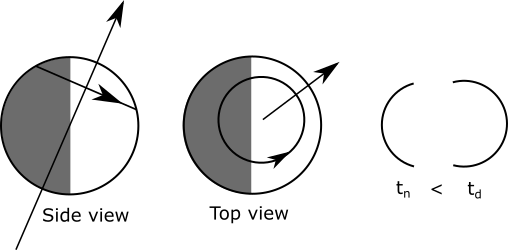
A line drawn perpindicular to the orbital plane through the center of the orbit will pass through what are called the orbit's ecliptic poles. The north and south ecliptic poles are designated relative to the direction of the planet's motion around the sun by the right-hand rule:
[diagrams of the above]
In galactic coordinates, Earth's ecliptic north pole is located at l = 97°, b = +30° (30 degrees above the galactic plane).
The IJK unit vectors of the geocentric-equatorial coordinate system are located, by definition, at:
l b
I 0 0
J 90 0
K () 90
The Xω, Yω, and Zω vectors in the heliocentric-ecliptic coordinate system have the same ecliptic longitude and latitude as their counterparts do right ascension and declination. The ecliptic and equatorial frames share the same I/Xω axis, and their K/Zω axises are (by definition) separated by the value of Earth's axial tilt, 23.4 degrees. The ecliptic frame is rotated in the positive K-direction from the J-axis:
l b
I 96.33727 -60.18850
J 206.98913 -11.42449
K 122.93194 27.12830
Xω 96.33727 -60.18850
Yω 186.37245 -0.02012
Zω 96.38398 29.81149
The celestial north pole (CNP) is identical with K, and the ecliptic north pole (ENP) is identical with Zω. Using these angles, we are ready to complete our 3D model.
I used the free 3D image software Blender to create the 3D model. For this, I needed models of the Earth (a sphere) and the orbital plane (the image above). [image]
I imported the image of the Milky Way Galaxy from the Introduction to serve as the background (bottom, really) of the image. A large black sphere serves as Sgr A*. [image]
A rod was added to the Earth sphere to show its rotational axis, and this was then rotated by [angles] to obtain its proper orientation. A map of Earth was applied to the sphere to give it the right appearance. [image]
Finally the orbit map was rotated into position by [angles] to produce the final product:
[image]
[1] "First" point because that was also coincidentally where the Sun entered Aries at the time.
[2] Hence this section is titled simply "Ecliptic coordinate system", identifying only the fundamental plane and not the center as well.
[3] Remember, only the Earth's orbital plane really "exists". The ecliptic is merely the Sun's apparent path seen from Earth's position on this plane.
[4] M. T. Karim, Eric E. Mamajek, Revised geometric estimates of the North Galactic Pole and the Sun's height above the Galactic mid-plane, Monthly Notices of the Royal Astronomical Society, Volume 465, Issue 1, 11 February 2017, Pages 472–481, https://doi.org/10.1093/mnras/stw2772. Value given as 17 ± 5 pc (parsecs); converted to light-years (ly) via 1 pc = 3.26 ly.
[5] Technically it's once every 23 hours 56 minutes, but the difference between solar and sidereal time is not of significance for this overview.
[6] [Mueller, Bate, White citation]